알고리듬 Dijkstra algorithm with direction을 알아보겠습니다.

Dijkstra(다익스트라, 데이크스트라) 알고리듬은 최단거리를 구할 때 사용합니다.
각 지점 간의 거리를 계속해서 업데이트합니다.
이번 시간에는 방향성이 있는 경우를 다뤄봅니다.

개념은 간단합니다. 미탐험 지역은 큰 값을 주고, 탐험한 지역은 가중치에 따라서 업데이트합니다. 더 작은 값이 발견되면 작은 값으로 수정합니다. 프로그램이 종료되면 전체 노드에 대한 최소 가중치를 얻을 수 있습니다.

아래와 같은 지점이 표시되어 있는 방향이 표시되어 있는 지도에서 3 -> 5로 가는 최단 거리를 구해보겠습니다.

각 지점 간의 관계는 다음과 같이 표시하기로 합시다.

[시작 지점, 거리, 도착 지점]

3 번 지점의 경우 [3, 2, 1], [3, 5, 4]

4 번 지점의 경우 [4, 1, 5]

지점은 총 5 개가 있고, 출발 지점은 3 번입니다. 도착 지점은 5 번입니다.

맵은 다음과 같이 있습니다.

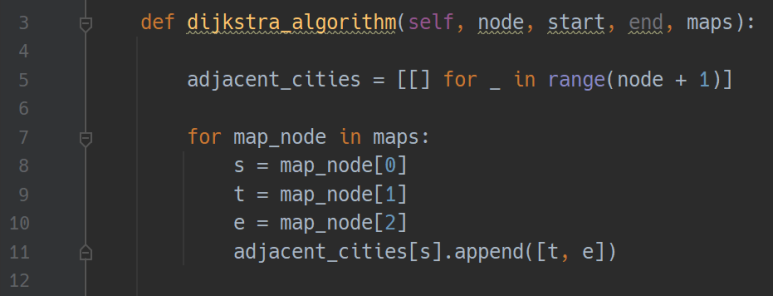
일단 모든 노드들의 관계를 저장할 리스트를 하나 만듭니다. 저는 adjacent_cities로 만들었습니다.

5 번째 줄에서 node + 1을 하는 이유는 리스트는 0부터 시작하지만 여기서 node는 1부터 시작하기 때문입니다.

맵에서 각 노드들의 정보를 가져온 다음, 해당 노드 위치에 시간과 목적지 노드를 추가합니다.

3 번 노드의 경우 두 개의 리스트를 원소로 가지게 됩니다.

그다음 전체 소요 시간을 관리할 리스트 하나 만듭니다. 아직 미지의 지역이기 때문에 큰 값을 넣어줍니다.

그리고 현재 시작 노드인 3은 소요 시간을 0으로 만들어줍니다.

그다음 우리가 탐방할 곳을 큐(Queue)로 관리할 거라서 Queue를 import 해줍니다.

이제 탐험할 노드를 관리할 Queue를 하나 만들고 거기에 처음 시작 노드를 넣습니다.

우리의 여정은 explore_node가 다 바닥날 때까지 돌아다니면 됩니다.

23 번째 줄에서 현재 노드를 가져옵니다.

25 번째 줄에서는 현재 노드와 연결된 정보들을 for 문을 통해서 불러옵니다.

29 번째 줄은 우리가 알고 있는 다음 노드의 소요 시간과 현재 노드 시간 더하기 여기서 다음 노드까지의 소요 시간을 비교하여 현재 노드에서 가는 경로가 더 시간이 적게 걸릴 경우 우리가 알고 있는 소요 시간을 짧은 시간으로 최신화 합니다. 그리고 최신화가 되었으니 우리의 여정에 최신화가 된 노드를 추가합니다.