수학 나머지 연산 역원(Modular multiplicative inverse)
수학 나머지 연산 역원(Modular multiplicative inverse)를 알아보겠습니다.
나머지 연산 글에서 나눗셈은 적용되지 않는다는 사실을 알았습니다.
그래서 우리는 역원을 이용하여 곱셈을 활용해야 합니다.
역원이란 둘을 곱했을 때, 1이 되는 수를 말합니다.
5의 역원은 1/5입니다.
이것을 나머지 연산에 표현하면 이렇게 표현합니다.
나머지 연산의 역원은 다음과 같은 방법으로 구합니다.
A^-1 자리에 0~(M-1)까지 숫자를 넣어가면서 1이 되는 것을 찾습니다.
24 mod 11의 역원을 찾아봅시다.
위의 그림에서 6을 곱했을 때 나머지가 1이 나옵니다. 따라서 24 mod 11의 역원은
6이 됩니다.
그럼 위의 나눗셈 식을 다시 해볼까요?
48/24 mod 11을 역원을 이용해서 곱셈 법칙으로 계산 가능합니다.
역원이 존재하기 위해서는 조건이 필요합니다. A와 M이 최대 공약수가 1 인
서로소여야 합니다.
유클리드 호제법(Euclidean algorithm)을 사용하면 최대 공약수가 1인 것을 쉽게
찾을 수 있습니다.
우리가 역원을 찾던 행위를 확장 유클리드 호제법을 사용하면 수식으로 표현할 수
있습니다.
여기서 y가 A^-1이 됩니다.
그리고 만약 M이 소수인 경우에는 페르마의 소정리(Fermat's little theorem),
오일러 정리(Euler's theorem)를 이용하여 쉽게 구할 수 있습니다.
페르마의 소정리는
p가 소수이고 a와 p가 서로소일 때 아래의 식이 만족한다고 합니다. 물론 b처럼
일반 정수일 때에도 성립되는 경우가 있기 때문에 역이 p가 소수라는 것을
보장하지 않습니다.
여기에 오일러 정리를 사용하여 일반화를 시킵니다.
a와 n이 서로소인 양의 정수일 때, 아래 식이 성립한다고 합니다.
아래에서 사용된 파이는 파이 함수입니다. 아래 게시글에서 확인 가능합니다.
그러면, ∮(n)에서 n이 소수이면 ∮(n) = n-1 개가 됩니다.
즉 n이 소수라면 페르마의 소정리와 같이 표현됩니다.
여기에 a의 역원을 구하게 되면 이렇게 됩니다.
즉 a^n-2 만 구하면 됩니다.
위에서 구한 24 mod 11의 역원을 오일러 정리로 구해봅시다.
똑같이 6이 나옵니다.
끝.
카테고리: Math

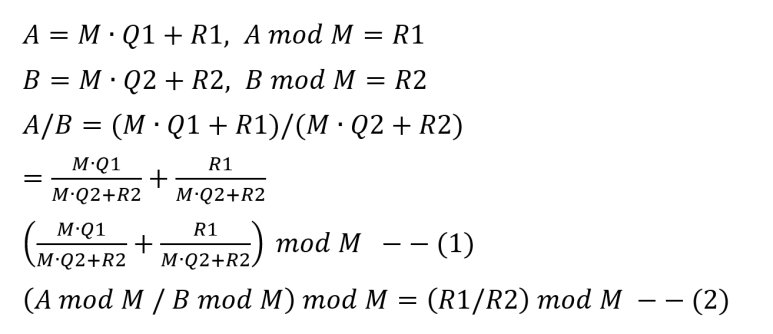





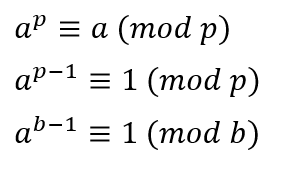













댓글
댓글 쓰기
궁금한 점은 댓글 달아주세요.
Comment if you have any questions.