Algorithm Merge sort

알고리듬 Merge sort를 알아보겠습니다.

​
합병 정렬(Merge sort)는 숫자를 잘게 분할해서 정렬을 하면서 다시 합치는 알고리듬입니다.
그냥 정렬하면 되는데, 왜 분할을 하냐 하면, 작은 문제를 풀면 큰 문제가 풀리는 놀라운 인생의 진리가 아닐까요?
걸리는 시간 Big O는 n log n입니다.
​
글로 설명하기보다는 아래 그림을 통해서 설명을 해볼게요.
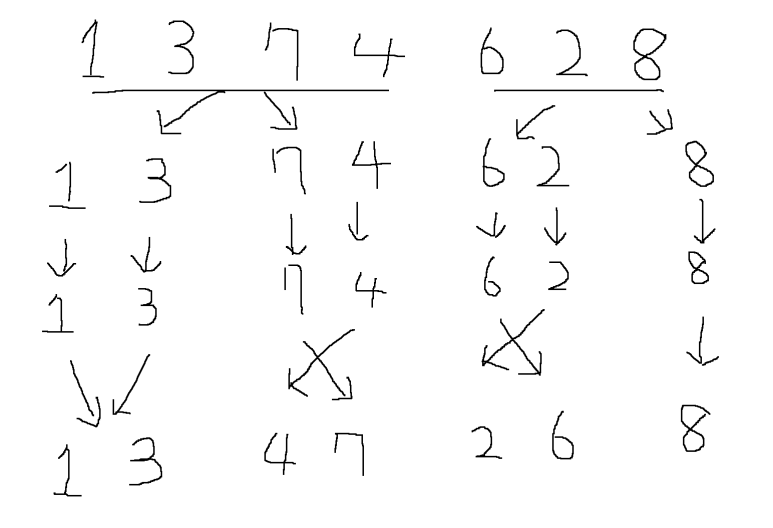
1, 3, 7, 4, 6, 2, 8 배열이 있습니다.

합병 정렬(Merge sort)를 진행해 봅시다.

1, 3, 7, 4와 6, 2, 8로 나눕니다.

그리고 다시 1, 3, 7, 4는 다시 1, 3과 7, 4로 나눕니다. 6, 2, 8은 다시 6, 2와 8로 나눕니다.

다음은 1, 3, 7, 4, 6, 2, 8 모두 각각 한자리로 나눕니다. 더 이상 나눌 수가 없으니 합칩니다.

다시 합치면서 정렬합니다. 

1, 3과 4, 7과 2, 6과 8로 정리되었습니다.

합칩니다. 순서가 오름차순으로 잘 되어있어서 달라질 게 없군요.

짜잔. 1, 2, 3, 4, 6, 7, 8로 정리가 됩니다.

이것을 코드로 한번 봅시다.

merge_sort라는 함수를 만듭니다. 인자로는 배열, 왼쪽, 오른쪽을 받습니다.

3 번째 줄에서는 왼쪽이 오른쪽보다 크거나 같으면 종료합니다.

위의 사진에서 보듯이 반을 나눠서 정렬을 진행해야 하므로 6 번째 줄에서 가운데를 찾습니다. 그리고 다시 가운데를 기준으로 앞뒤로 나눠 merge_sort를 진행합니다.

위의 작업은 작은 단위로 나누는 작업만 포함되어 있습니다.

실제적으로 정렬하면서 합치는 과정을 다룰 함수를 하나 만듭니다.

14 번째 줄에서 나눠진 왼편의 개수를 구합니다. 

15 번째 줄에서 나눠진 오른편의 개수를 구합니다.

​

17 번째 줄에서 왼편의 값을 담을 리스트를 하나 만듭니다.

18 번째 줄에서 오른편의 값을 담을 리스트를 하나 만듭니다.

20 번째 줄과 23 번째 줄에서 각각 원래 배열의 값을 담습니다.

left_index, right_index, current_index를 설정합니다. 정렬이 시작될 위치는 가장 낮은 값이므로 current_index에 left를 넣습니다.

​

28 번째 줄에서 양쪽 중에 어느 하나가 전부 소진될 때까지 정렬을 합니다.

29 번째 줄에서 만약 왼편 처음 값이 오른편 처음 값보다 작다면 원래 배열에 왼편 값을 넣습니다.

33 번째 줄에서 그렇지 않다면, 원래 배열에 오른편 값을 넣습니다.

이제 어느 한쪽이 다 소진되면, 나머지는 정렬된 상태일 것이므로 그냥 뒤에 붙여줍니다. 우리는 어느 쪽이 남았는지 모르므로 둘 다 적어줍니다.

이제, merge_sort 함수에도 9 번째 줄처럼 merge_merge 함수를 적어줍니다.

이제, 실행해 봅시다.

끝.

카테고리: Algorithm