Algorithm LIS(Longest Increasing Subsequence)

알고리듬 LIS(Longest Increasing Subsequence)를 알아보겠습니다.

LIS 한글로 하면, 최장 증가 부분 수열입니다.
순차로 값이 증가하는 수열 중에 가장 긴 값이 무엇인지 찾는 알고리듬입니다.
​
1,5, 6, 5, 8, 3, 2 이렇게 수열이 존재한다면. 증가하는 수로 이뤄진 가장 긴 부분 수열은 1, 5, 6, 8이 됩니다.
​
어떻게 최대 길이가 되는 것을 찾는지 알아봅시다.
처음에는 1을 넣습니다.

다음 5를 봅니다. 5 도 넣어줍니다.

다음 6을 봅시다. 6 도 넣어줍니다.

5를 봅니다. 5가 있으므로 5의 자리에 새로운 5를 집어넣습니다. 결과적으로는 변화가 없습니다.

다음 8을 봅니다. 8도 추가해 줍니다.

3을 봅니다. 3의 위치는 1 다음에 위치해야 하므로 5 대신에 3을 넣습니다.

2를 봅니다. 2는 1 다음에 와야 하므로 3 대신에 2를 넣습니다.

따라서, 최장 증가 부분 수열의 크기는 4입니다.

하지만, 현재 값이 최장 증가 부분 수열이 가장 클 때 값이 아니군요. 가장 클 때 값은 1, 5, 6, 8인데 말이죠.

​

​

그렇다면, 1, 5, 6, 8은 어떻게 구할까요?

부분 수열에 저장될 때 위치 값을 같이 저장해 줍니다.

인덱스를 같이 표기하면 아래와 같이 됩니다.

부분 수열의 크기는 4입니다. 그래서, 3, 2, 1, 0를 뒤에서부터 구하면 가장 클 때의 값이 구해집니다.

1, 5, 6, 8

​

​

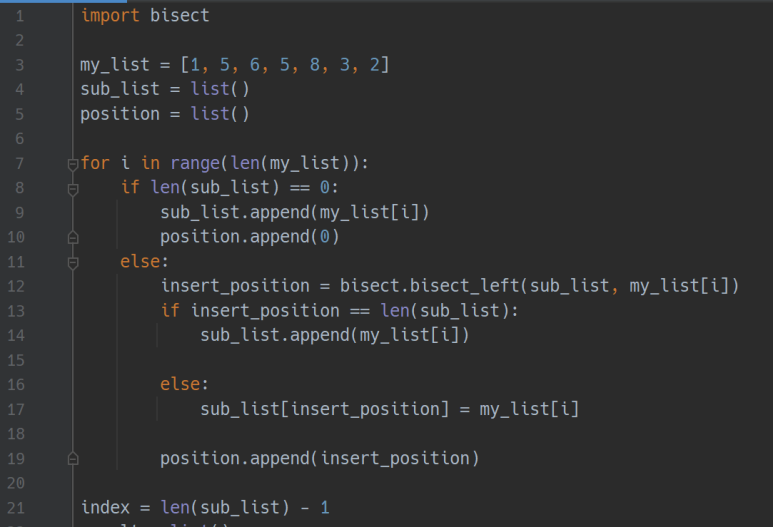
코드로 한 번 볼까요?

2진 탐색을 위해 bisect를 사용합니다.

12 번째 줄에서 해당 숫자가 들어가야 할 위치를 bisect_left로 찾습니다.

13 번째 줄에서 들어가야 할 위치가 마지막 부분이면 추가를 해줍니다.

17 번째 줄에서 들어가야 할 위치가 중간 부분이면 중간 부분 값을 지금 숫자로 변경합니다.

19 번째 줄에서 위치 값들을 저장합니다.

21 번째 줄에서 부분 수열의 크기를 구합니다.

28 번째 줄에서 저장된 위치의 숫자이면 추가해 줍니다.

끝.

카테고리: Algorithm